L'univers semble
infiniment grand... et infiniment petit ! Sans parler des autres infinis : ceux
de l'intériorité, de l'imagination, du temps, du rien (?)...
Un site donne à voir plusieurs animations dans cet esprit :
Les tailles dans l'univers.
Un zoom sur une figure fractale :
quelque soit la puissance du zoom, on finit par retrouver la même forme (celle
de Mandelbrot).
L'homme semble disproportionné dans ces infinis. Mais qui est ainsi
"dans" ? Car, comme l'a si bien dit Pascal (qui, par ailleurs
"pompait" allègrement Montaigne et Bovelles),
ces espaces sont contenus dans l'espace conscient. Ce que l'on peut joliment
illustrer :
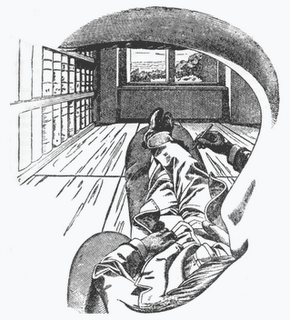
Il est aisé de voir que l'espace conscient englobera toujours les formes,
quelque soit l'échelle de ce qui est vu.
Évidemment, cela ne tient que si l'on identifie réalité et représentation.
Mais peut-on faire autrement ? Se représenter une réalité extérieure à toute
représentation, n'est-ce pas encore une représentation ? La chose représentée,
qu'elle soit subjective ou objective, semble ainsi devoir toujours être identique
à sa représentation. D'un autre côté, se représenter, n'est-ce pas
nécessairement se représenter quelque chose qui est autre que cette
représentation ? Existe t-il une représentation qui ne soit pas
"représentation de" ?
J'en conclu que la dualité comme l'identité pure sont fausses. La dualité est
une erreur. L'unité à l'exclusion de la dualité en est une autre. La
formulation de la Reconnaissance
me paraît plus juste :
"L’apparition, « à l’extérieur » (de la conscience), des phénomènes qui sont en ce moment même apparents n’est possible que s’ils existent « à l’intérieur » (de la conscience).
Même dans la perception directe (d’un objet), l’apparence des objets en tant que séparés (du sujet) n’est possible que dans la mesure où ceux-ci sont immergés dans le sujet connaissant."
Utpaladeva, Stances pour reconnaître le Seigneur en soi, V, 1